Георг Симон Ом и первый закон электродинамики

  Сейчас трудно себе представить, насколько тяжело было тогда создавать электромагниты. Ведь даже закон Ома инженерам в то время не  был известен. 

Георг Симон Ом (16.03.1787 - 6.07.1854) - немецкий физик, член-корреспондент Берлинской АН. Окончил Ирландский университет. Преподавал математику затем физику в различных гимназиях. С 1833 - профессор Нюрнбергской высшей политехнической школы. В 1849-52 - ректор Мюнхенского университета. Член Лондонского королевского общества. Медаль Копли (1841).
Исследования относятся к электричеству, акустике, оптике, кристаллооптике. Экспериментально открыл в 1826 основной закон электрической цепи, связывающий между собой силу тока, напряжение и сопротивление (закон Ома). В 1827 вывел его теоретически (для участка и полной цепи), ввел понятия "электродвижущей силы", падения напряжения", и "проводимости". Выполнил (1830) первые измерения э.д.с. источника тока. 

Когда немецкий учитель Георг Симон Ом положил на стол ректора Берлинского университета свою диссертацию, где впервые был сформулирован закон, без которого невозможен ни один электротехнический расчет, он получил весьма резкую отповедь. Электричество-де не поддается никакому математическому описанию, так как «электричество – это собственный гнев, собственное бушевание тела, его гневное Я, которое проявляется в каждом теле, когда его раздражают». Ректором Берлинского университета был в те годы Георг Вильгельм Фридрих Гегель.

Ом - О законе постоянного тока

ОПРЕДЕЛЕНИЕ ЗАКОНА, ПО КОТОРОМУ МЕТАЛЛЫ ПРОВОДЯТ КОНТАКТНОЕ ЭЛЕКТРИЧЕСТВО, ВМЕСТЕ С НАБРОСКОМ ТЕОРИИ ВОЛЬТАИЧЕСКОГО АППАРАТА И МУЛЬТИПЛИКАТОРА ШВЕЙГГЕРА

<...> И поэтому я обратился к использованию термоэлектрической батареи, пригодность которой для моих целей была указана г-ном Поггендорфом; и поскольку полученные на этом пути результаты отчетливо дают закон проводимости, я думаю, что не будет чрезмерным подробное описание моего прибора, чтобы степень доверия к полученным с его помощью результатам могла быть оценена с большей легкостью.

Кусок висмута был отлит в форме прямоугольной скобы abb'а', длинная сторона которой равна 6¹/₂ дюйма, а короткие ножки аb и а'b' были по 3¹/₂ дюйма. Она была рассчитана в 9 линий шириной и 4 линии толщиной. К каждой из ножек с помощью двух винтов я прикрепил медные полоски abcd, a'b'c'd', которые имели ширину 9 линий, толщину 1 линию, а их общая длина составляла 28 дюймов. Полоски были изогнуты так, что их свободные концы cd, c'd' погружались в ртуть, находившуюся в двух чашечках m, m', стоявших на деревянном основании fghi.

На верхней пластине основания помещался крутильный подвес, в описании которого я буду немного более распространенным, поскольку его конструкция несколько отличается от обычной. Стеклянный цилиндр, на котором установлен подвес, имел 6 дюймов в высоту и 4¹/₂ дюйма в ширину. Сам подвес состоял из двух частей, одна из которых, nop, снабжена гнездом, сделанным слегка на конус, и накрепко приклеена к верхней пластинке стеклянного цилиндра, вторая часть, grs, с коническим выступом толщиной 8 дюймов, плотно входящим в гнездо, и с пластинкой rr шириной 3 дюйма покоилась на пластинке n той же ширины. В средней точке выступа qs на токарном станке с большой тщательностью было сделано небольшое конусообразное углубление, которое затем было заполнено металлом на ¹/₂ дюйма своей длины так, что плоские поверхности, образованные таким образом, придавали коническому углублению вид полного треугольника. С помощью специальных приспособлений нить, на которой подвешивалась игла, прикреплялась к выступу, причем так, что средняя точка иглы попадала в точности под вершину треугольника.  

Магнитная игла tt была сделана из стальной проволоки толщиной 0,8 линии и имела длину около 2 дюймов. Ее концы были вставлены в цилиндры из слоновой кости, к одному из которых прикреплялась латунная проволока, заостренная и слегка загнутая вниз. Этот латунный указатель, служащий индикатором, расположен вблизи латунной дуги ии, покоящейся на деревянном основании и разделенной на градусы. Сначала я сделал магнит столь длинным, что его конец двигался непосредственно над градуированной шкалой. Однако затухающий характер его движения, на что указывает малое число совершаемых им колебаний, напомнил мне об экспериментах, недавно проведенных Араго, и заставил меня избрать другую схему.  

Таким образом, изготовленная игла подвешивалась на полоске из расплющенной золотой проволоки 5 дюймов длиной, которая прикреплялась к крутильному подвесу в точности по оси вращения. Такие резиноподобные металлические полоски, на мой взгляд, гораздо лучше подходят для экспериментов с крутильным подвесом, чем цилиндрические проволоки. Полоска, которую я использовал в своих крутильных весах, не говоря о ее малой длине, которая, по моему мнению, весьма желательна, в столь высокой степени отвечает всем требованиям, [предъявляемым] к исследованиям с крутильными весами, что после того, как полоска подвергалась усилию, соответствующему более чем трем полным оборотам, при освобождении нагрузки она принимала свое первоначальное положение. Тем не менее после каждого опыта я определял положение равновесия иглы, чтобы убедиться, что в приборе не произошло никаких изменений. Более того, я полагаю, стоит отметить, что опыты, проведенные с похожей латунной иглой, убедили меня, что малые и большие колебания (я исследовал их от двух полных оборотов до нескольких градусов) происходят в точности за одно и то же время, так что в этом отношении здесь нечего опасаться.

Крутильный подвес был приклеен к верхней пластинке основания так, что прямая линия, проведенная поперек латунной полоски bc в направлении центральной точки градуированной дуги и простой шелковой нити, натянутой перпендикулярно этой дуге, лежала в плоскости магнитного меридиана, так же как и магнитная игла, когда ее указатель был направлен на нуль шкалы. На выступе основания k находилась выпуклая линза с фокусным расстоянием в один дюйм, установленная таким образом, чтобы [с ее помощью] могла наблюдаться нижняя градуированная шкала. Для того чтобы избежать параллакса, глаз в процессе наблюдения всегда помещался так, чтобы шелковая нить и средняя точка шкалы совпадали. Наблюдения проводились следующим образом. Как только игла отклоняется под действием электрического тока в приборе, полоска закручивается в противоположную сторону с помощью вращающейся части подвеса до тех пор, пока латунный указатель иглы не встанет за шелковой нитью напротив средней точки шкалы. Затем закручивание считывается по верхней шкале с точностью до сотых долей оборота, число которых, как известно, дает силу, которая действует на иглу.

Концы проводников, использовавшихся в эксперименте, были опущены в чашечки с ртутью m, m', над которыми для большей уверенности располагалось простое устройство, гарантировавшее, что концы каждого проводника всегда одинаково находились в контакте со ртутью. Вдобавок концы проводников, когда имелась какая-либо причина опасаться контакта со ртутью, покрывались канифолью, а торцевые поверхности начисто стачивались напильником и постоянно обновлялись.

Совершенный металлический контакт различных частей — необходимое условие в исследованиях этого рода, поскольку в противном случае наблюдения не будут согласовываться между собой.

Наконец, для того чтобы придать частям прибора, где в контакте находятся висмут и медь, нужную разность температур, я изготовил два оловянных сосуда, сечения которых в увеличенном масштабе показаны на рисунке.

Каждый из них имел в своей средней части пространство хх, открытое сверху, а в других частях полностью закрытое для вставления в него ножек ab, a'b'. В сосуде А вода постоянно поддерживалась в состоянии кипения. Этот сосуд имел отверстие у, которое могло закрываться пробкой и через которое в него наливалась вода; с другой стороны находилась трубка zz, через которую выходил пар. В сосуд В помещался снег или кусочки льда. Ножки аb, a'b' зашивались в тонкий, но плотного плетения шелк, а затем вставлялись в выемки хх, которые вслед за этим наполнялись до высоты примерно в один дюйм мелкой дробью, их верхняя часть заполнялась после этого толченым стеклом. В этих условиях все точки контакта висмута и меди находились в области, заполненной свинцом, который хорошо проводит тепло, а слой стекла защищал эту область от быстрых изменений температуры, обусловленных окружающим воздухом.

После этого подробного описания прибора я перехожу к экспериментам, которые провел с его помощью. Я изготовил восемь различных проводников 1, 2, 3, 4, 5, 6, 7. 8, имевших длину соответственно 2, 4, 6, 10, 18, 34, 66, 130 дюймов и толщину ⁷/₈ линии, вырезанных из одного куска полоскового медного провода, приготовленного описанным выше способом. После того как вода кипела на протяжении получаса, эти провода один за другим включались в цепь. Между любыми двумя сериями экспериментов, которые длились от 3 до 4 ч, всегда делался часовой перерыв, когда некоторое количество уже подогретой воды доливалось [в сосуд А], вскоре эта вода начинала кипеть. Затем проводники вновь последовательно включались в цепь, но в обратном порядке. Таким образом я получил следующие результаты.  

Оказывается, что сила ощутимо уменьшается день ото дня. Я не осмеливаюсь решить, следует ли искать причины этого [различия] в изменении площади контактов или в том факте, что 8 и 15 января были очень холодными днями и коробка со льдом стояла на окне слабо обогреваемой и защищенной комнаты. Думаю, что необходимо добавить, что начиная с 15 января я больше не наблюдал подобных различий. 

Специально следует отметить тот факт, что нельзя заметить никаких следов колебаний, подобных возникшим при наличии в цепи гидроэлектрической батареи. Когда игла приходила в состояние покоя, она оставалась на своем месте без дальнейшего движения. Я часто следил за ней в течение получаса после проведения серии наблюдений и не отметил ни малейшего изменения ее положения. Вообще, когда игла при подключении проводника приходила в равновесие и удерживалась в этом положении стопором, помещавшимся по одну сторону от нее, то после замыкания цепи этим же проводником (вслед за его удалением на некоторое время из цепи) не наблюдалось ни малейшего движения [иглы] в противоположную сторону. Это подтверждает вывод, что колебания имели своим источником изменения в жидкости, которая обусловливает электрический ток сам по себе и поднимается и спадает вместе с ним. Кажется, как будто движущимся электричеством осуществляется разделение определенных составляющих жидкости, которое происходит в соответствии с теми же в точности законами, что и те, которые были определены для действия покоящегося электричества. Увеличение силы проявляется в возросшем разделении составляющих, уменьшение силы допускает частичное объедъинение, которое становится полным,

когда сила исчезает. Весьма вероятно, и мы позднее найдем подтверждение этой точке зрения, что разделение жидкости током создает изменение не только в возбуждающей силе цепи, но также и в проводимости жидкости, и именно эта изменчивость в контурах с гидроэлектрическими элементами делает законы проводимости в них такими путаными и столь трудно раскрываемыми. Как только мы пытаемся определить лишь влияние металлов на проводимость электрического тока, то сразу же становится ясно, что цепи с гидроэлектрическими элементами не подходят для этой цели, поскольку они порождают множество нерегулярностей; в то же время термоэлектрическая цепь полностью годится для этой цели. Сейчас мы увидим, что она дает.  

Уже приведенные числа могут быть весьма удовлетворительно представлены уравнением  
X=a/(b+x),
где X — это сила магнитного действия, возникающая при использовании проводника, х, а а и b— постоянные величины, зависящие от возбуждающей силы и сопротивления остальной части контура.

Если, например, мы положим b равным 20¹/₄ и а в различных сериях равным 7285, 6965, 6885, 6800, 6800, то путем расчетов получим следующие результаты [см. табл.]

Если мы сравним эти числа, найденные посредством расчета с предыдущей последовательностью чисел, найденной из опыта, то окажется, что разности очень малы и имеют порядок, который можно ожидать в исследованиях такого рода. Я не буду откладывать рассмотрение этого вопроса, но перейду к доказательству формулы в крайних случаях. Этот метод наиболее продуктивен для установления общей применимости закона, который был выведен из ограниченного числа случаев.

Для этого я сделал четыре проводника а, b, с, d соответственно 2,4,8, 16 дюймов длины из латунной проволоки толщиной 0,3 линии, которую я использовал в моих предшествующих исследованиях с гидроэлектрическими цепями; они дают в цепи числа 111¹/₂, 64³/₄, 37, 19³/₄, когда проводник 1 дает 305. Из приведенного выше уравнения можно определить длины, соответствующие этим числам. Мы нашли, что они равны 40³/₄, 84³/₄, 163¹/₂, 324. Эти значения в целом согласованно указывают, что 1 дюйм латунного провода эквивалентен 20¹/₂ дюймам расплющенного медного провода. После этой предварительной работы я ввел в цепь проводник из той же латуни длиной 23 фута (который в этой серии я обозначаю как номер 5); он дал 1¹/₄. И действительно, мы получаем почти в точности это значение, если для х в уравнении возьмем величину 23Ч12Ч20¹/₂=5658. На этом примере мы видим, что уравнение очень точно согласуется с опытом почти до того состояния, когда сопротивление проводников подавляет силу.

Далее я поддерживал один конец пары медь — висмут при температуре 0°R, используя лед, в то время как другой конец находился при комнатной температуре, которая, как показал термометр, висевший во время наблюдений рядом с прибором, оказалась стабильно равной 7¹/₂°R. Проводники, включенные в контур в последовательности 1, 2, 3, 4, 5, 6, 7, 8, 7, 6, 5, 4, 3, 2, 1 дали такие числа: 27, 25, 23¹/₃, 20, 15¹/₂, 10³/₄, 6¹/₂, 3²/₃, 6¹/₂, 10³/₄, 15¹/₂, 20, 23¹/₂, 25¹/₄, 27³/₄. Если мы подставим в наше уравнение b=20¹/₄ и так определим а, что a/22¹/₄=27³/₈, то путем расчета мы получим значения, которые ни в одном случае не отличаются от приведенных выше более чем на половину деления, откуда следует, что уравнение справедливо для любых значений возбуждающей силы. Из этого последнего исследования становятся очевидными еще два важных момента. Во-первых, примечательное обстоятельство заключается в том, что величина b остается неизменной, в то время как сила уменьшается более чем в 10 раз; так что а, по-видимому, зависит только от возбуждающей силы, а b — только от неизменяемой части цепи. Во-вторых, из этого эксперимента, видимо, следует, что сила термоэлектрического контура в точности пропорциональна разности температур его двух концов.

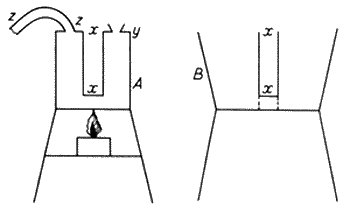
В заключение этого исследования я не могу удержаться от упоминания об одном наблюдении, которое в более непосредственной форме подтверждает вывод Дэви о том, что проводимость металлов возрастает с понижением температуры. Я брал 4 дюйма медного провода и включал его в цепь; он давал 159 делений. Когда я нагревал провод в его средней части пламенем спиртовки, сила постепенно падала на 20 делений и более и таким же было действие, когда я сдвигал пламя к одному или другому концу проводника; но когда я поместил его на слой снега, сила возросла на два деления. Температура в комнате была 8¹/₄ °R. Этот факт не кажется здесь не относящимся к делу, поскольку он может вызывать небольшие аномалии. <...> 

Время наблюдения

Серия опытов

Проводники

1

2

3

4

5

6

7

8

Янв. 8

I

326³/₄

300³/₄

277³/₄

238¹/₄

190³/₄

134¹/₂

83¹/₄

48¹/₂

Янв. 11

II

311¹/₄

287

267

230¹/₄

183¹/₂

129¹/₄

80

46

III

307

284

263³/₄

226¹/₄

181

128³/₄

79

44¹/₂

Янв. 15

IV

305¹/₄

281¹/₂

259

224

178¹/₂

124³/₄

79

44¹/₂

V

305

282

258¹/₄

223¹/₂

178

124³/₄

78

44